Pythagore

« En 1940, dans The Pythagorean Proposition, Elisha Scott Loomis a publié 371 démonstrations du théorème (de Pythagore), recueillies auprès d'une étonnante palette de contributeurs. L'une, datée de 1888, est attribuée à E. A. Coolidge, une jeune fille aveugle ; une autre, de 1938, à Ann Condit, lycéenne de 16 ans ; d'autres ont pour auteurs Léonard de Vinci ou le président américain James Garfield. »

« L'immense diversité de ces démonstrations témoigne de la vitalité des mathématiques. Il n'existe jamais de « bonne façon » d'aborder un problème, et il y a quelque chose de fascinant à retracer les différents cheminements qu'ont suivi différents esprits pour aboutir à la solution. En voici trois, provenant d'époques distinctes ; la première est de Liu Hui, mathématicien chinois du III^e siècle de notre ère ; la deuxième, de 1917, est celle d'Henry Dudeney, le plus célèbre compositeur de casse-tête britannique. »«  la dernière est attribuée à Léonard de Vinci (1452-1519). »

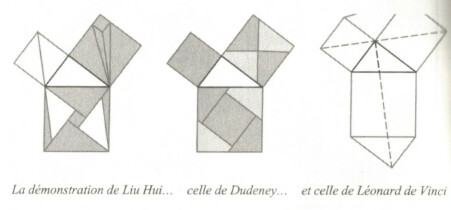
(Source : Alex au Pays des Chiffres par Alex Bellos (2010), traduit chez Robert Laffont)

Les deux premières démonstrations sont des puzzles de Pythagore, tandis que la troisième repose sur des calculs d'aires.

À propos du puzzle de Dudeney : on peut trouver ici une généralisation dynamique du puzzle en question (ne pas hésiter à diminuer la taille de la page web pour voir la figure en entier).

Un peu plus haut dans ce même texte :

« Celle qui suit est particulièrement charmante ; on la doit au mathématicien arabe Al-Nayrizi, et remonte probablement aux alentours de l'an 900 de notre ère. Le théorème est contenu dans la répétition du schéma. »

L'originalité de cette démonstration : elle est basée sur un pavage.

Mais cette fois le schéma n'a pas été reproduit, et c'est voulu ! Dans le paragraphe suivant une figure dynamique est proposée pour vous aider à retrouver la démonstration en question.