Pythagore

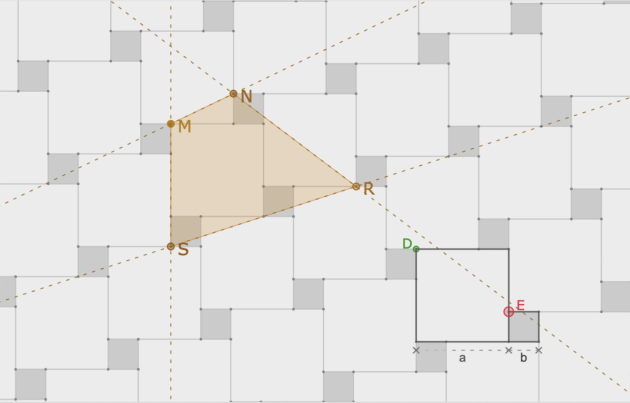
Ci-dessus : une simple image. Dans un autre onglet : la figure dynamique ... responsive ! (et exportable)

Le pavage double d'Al-Nayrizi est ici incomplet.

• Premier pavage (visible) : le pavé de base est formé par la réunion d'un carré blanc et d'un carré gris. On complète le pavage par simple translation de ces pavés. (Remarque : le point E est mobile)

• Second pavage imaginé par Al-Nayrizi, mais non représenté ici : le pavé de base est un seul et unique carré dont les sommets sont aussi sommets de carrés précédents. À vous de le trouver ! Comment ? En déplaçant les points M, N, R et S pour obtenir le carré en question. Si la réponse est bonne le maillage du pavage apparaît.

• En fait il n'y a pas un pavage solution mais quatre. Parmi ces quatre solutions (à trouver) on privilégiera celle pour laquelle le point D est un noeud de ce maillage.

• Une simple observation de la figure et en particulier de la répétition des motifs permet d'affirmer que l'aire du pavé du pavage n°2 est égale à la somme des aires des carrés du pavé n°1 ! En bref, que deux carrés peuvent être remplacés par un seul, à condition d'effectuer un découpage judicieux par deux simples coups de ciseaux. Vous ne voyez toujours pas ? Le déplacement des pièces de puzzle apparues en même temps que le maillage devrait vous aider à le réaliser.