La figure DGPad
Réciproque et contraposée
Avant de proposer aux élèves la figure ci-dessous, il pourrait être bien utile de leur suggérer de visionner deux petites vidéos (destinées aux élèves de cinquième et au-delà évidemment !)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Conseil :
Si ces vidéos vous ont plu, pourquoi ne pas vous abonner à la chaîne d'Éric ? Au jour de la rédaction de cet article (mai 2021) il y a 97 vidéos destinées aux élèves de cinquième.
La figure DGPad
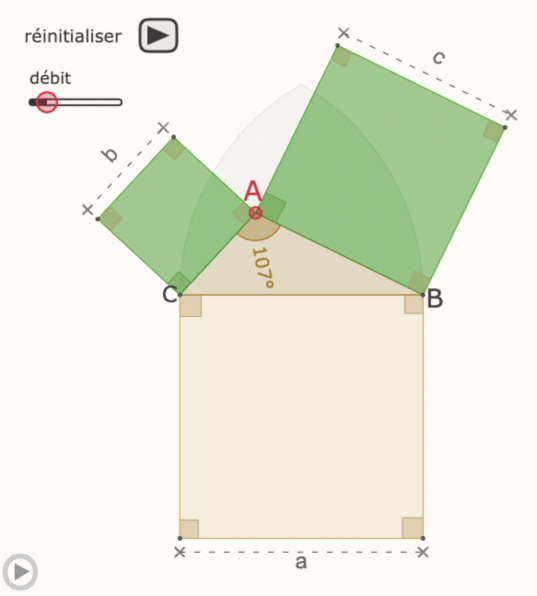
Ci-dessus : une simple image. Dans un autre onglet : la figure dynamique ... responsive !
Avant de bouger le point A il est conseillé de stopper l'animation et de réinitialiser.
Remarque :
Quelques remarques à propos de cette figure :
Il faut imaginer cette figure en 3D, avec une épaisseur de
1. Auquel cas, numériquement parlant (sans tenir compte des unités) les mesures des surfaces et volumes sont les mêmes. Le liquide circule entre les « carrés ».Il s'agit d'utiliser le liquide contenu dans les deux plus petits « carrés » pour remplir si possible le plus grand.
C'est pourquoi le plus grand côté BC (de mesure \(a\)) est dessiné à l'horizontale, et que le point A est contraint à l'intérieur d'une zone délimitée par deux cercles de rayon \(a\) ; il se trouve aussi dans demi-plan supérieur de frontière (BC). Toutes les formes de triangles sont quand même possibles.
Méthode : Suggestions d'utilisation
pour le théorème direct (le point A est aimanté par le demi-cercle de diamètre BC)
pour le théorème réciproque :
soit un triangle ABC de plus grand côté \(a\) (notations classiques) ; s'il n'est pas rectangle, alors \(a^2\) est différent de \(b^2+c^2\)
On passe alors à la contraposée : si \(a^2=b^2+c^2\) alors il est rectangle en A.